Методика корреляционного анализа

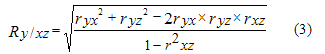(9)

Этот коэффициент изменяется от 0 до 1. Если элиминировать (совсем исключить или зафиксировать на постоянном уровне) влияние на и , то их "общая" связь превратится в "чистую", образуя чистый (частный) коэффициент линейной корреляции Пирсона:

(10)

Этот коэффициент изменяется от -1 до +1. Квадраты коэффициентов корреляции (2)-(4) называются коэффициентами (индексами) детерминации - соответственно парной, чистой (частной), множественной (совокупной):

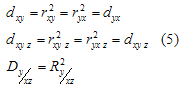(11)

акция доходность прогнозирование

Каждый из коэффициентов детерминации изменяется от 0 до 1 и оценивает степень вариационной определенности в линейной взаимосвязи переменных, показывая долю вариации одной переменной (y), обусловленную вариацией другой (других) - x и y. Многомерный случай наличия более трех переменных здесь не рассматривается.

Согласно разработкам английского статистика Р.Э. Фишера (1890-1962), статистическая значимость парного и чистого (частного) коэффициентов корреляции Пирсона проверяется в случае нормальности их распределения, на основании -распределения английского статистика В.С. Госсета (псевдоним "Стьюдент"; 1876-1937) с заданным уровнем вероятностной значимости и имеющейся степени свободы , где - число связей (факторных переменных). Для парного коэффициента имеем его среднеквадратическую ошибку и фактическое значение -критерия Стьюдента:

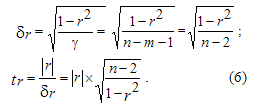(12)

Для чистого коэффициента корреляции при расчете его вместо (n-2) надо брать , т.к. в этом случае имеется m=2 (две факторные переменные x и z). При большом числе n>100 вместо (n-2) или (n-3) в (6) можно брать n, пренебрегая точностью расчета.

Если tr > tтабл. , то коэффициент парной корреляции - общий или чистый является статистически значимым, а при tr ≤ tтабл. - незначимым.

Значимость коэффициента множественной корреляции R проверяется по F - критерию Фишера путем расчета его фактического значения

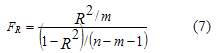(13)

При FR > Fтабл. коэффициент R считается значимым с заданным уровнем значимости a и имеющихся степенях свободы и , а при Fr≤ Fтабл - незначимым.

В совокупностях большого объема n > 100 для оценки значимости всех коэффициентов Пирсона вместо критериев t и F применяется непосредственно нормальный закон распределения (табулированная функция Лапласа-Шеппарда).

Другие материалы

Типы конкуренции и основные рыночные структуры в современной экономике
В конце XX столетия наша страна вступила на путь перехода от плановой системы экономики к рыночной, неотъемлемой частью которой является конкуренция как необходимое условие развития предпринимательской деятельности. Главной особенностью рын ...

Анализ и оценка эффективности использования основных средств (на примере УП Гомельское отделение Белорусской железной дороги)
Основные средства являются одним из важнейших факторов любого производства. Их состояние и эффективное использование прямо влияет на конечные результаты хозяйственной деятельности предприятий. Развитие рыночных отношений предполагает конкурентну ...