Результаты вычисления интервальных оценок для математического ожидания и дисперсии
Для вычисления интервальной оценки математического ожидания воспользуемся формулой:
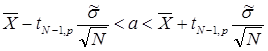, (1.11)
где а = М(Х) - математическое ожидание, tn−1,p - процентная точка распределения Стьюдента с n-1 степенью свободы; p - доверительная вероятность.
Подставляем в формулу вычисленные ранее значения 
,
и N. В результате получим:
Задаёмся доверительной вероятностью 
; 
Для каждого значения 
(i=1,2) находим по таблице (приложение А) значения 
и вычисляем два варианта интервальных оценок для математического ожидания.
При 
находим 
Доверительный интервал для а = М(Х) имеет вид: 40,9403 < a < 43,4397.
При 
находим 
Доверительный интервал для а = М(Х) имеет вид: 40,528 < a < 43,852
Для интервальной оценки дисперсии существуют следующие неравенства:
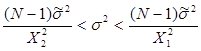(1.12)
Подставляем в неравенство известные значения N и 
получим неравенство, в котором неизвестны 
и 
.
Задаваясь доверительной вероятностью 
(или уровнем значимости а) вычисляем значения 
и 
. Используем эти два значения и степень свободы V=N-1 по таблице находим 
и 
и 
- это границы интервала, в который попадает случайная величина Х, имеющая 
распределение вероятности 
и заданной степени свободы V.
Для 
=0,95, (1 - р1)/2 = 0,025, (1 + р1)/2 = 0,975 и V=59 находим по таблице (приложение Б):
Подставляя в неравенства и 
и произведя вычисления, получим интервальную оценку:
,609
34,179
Для 
,
; 
и V=59 находим по таблице приложения Б:
Другие материалы
Технико-экономическое обоснование разработки газового месторождения
Система
газоснабжения России - основополагающий элемент национальной экономики, от
надежного и эффективного функционирования которого непосредственно зависит ее
нормальная работа и жизнеобеспечение всех граждан России. Газовая отрасль
занимает ...
Теория монополий и проблема рыночной власти
В
индустриально развитых странах Запада в результате действия многообразных,
часто противоречивых тенденций развития производительных сил складывается
разнообразная структура рыночных отношений, а также форм и методов конкуренции
и регулировани ...
