Статистический анализ точности и стабильности технологического процесса

Проводим математическую статистическую обработку результатов измерений.

Определяем точечные оценки координаты центра распределения и СКО результатов наблюдений и измерений.

Определяем выборочное среднее арифметическое () по формуле:

,

где X i - отдельные результаты наблюдений;

n - общее количество результатов наблюдений.

Определяем среднее арифметическое 90%-ной выборки ()

Среднее арифметическое находится по формуле:

,

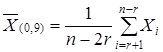где 2r- число не учитываемых результатов. Пять процентов выборки в нашем случае 0,05∙n = 0,05∙20=1, т.е. один результат измерения. Отбрасываем по одному измерению с концов вариационного ряда, т.е. результаты x1 = 73,91% и x19 = 75,69%.

Определяем медиану наблюдений ()

Медианой называют наблюдаемое значение Xi (так называемую варианту), которая делит вариационный ряд на две части, равные по числу вариант.

При n - нечётном:

%;

%;

Срединный размах вариационного ряда определяем по формуле:

,

где x0.25; x0.75 - 25% и 75%-ные квантили опытного распределения (представляют собой усредненные значения конкретных результатов наблюдений).

Вычисляем 25% и 75%-ные квантили опытного распределения. Этими квантилями являются точки между 4 и 5, а также между 16 и 17 результатами:

%;

%;

Тогда:

%;

Центр размаха определяется по формуле:

%;

%;

Полученные оценки центра распределения располагаем в вариационный ряд: 74,93<74,94<74,94<74,8<75,11%.

За оценку распределения (результата измерения) окончательно принимаем серединный размах вариационного ряда, так как эта оценка занимает медианное положение в ряду оценок:

=%.

Определение оценок среднеквадратического отклонения

Проверим присутствие грубых погрешностей в данной совокупности. Найдем среднеквадратическое отклонение (S) всех представленных результатов наблюдений: статистическиий показатель качество хлеб

%;

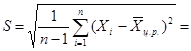
Оценку СКО результатов измерений определяем по формуле:

%;

Таблица 5

Выборка №2, результаты наблюдений

Другие материалы

Статистический анализ точности и стабильности технологического процесса производства хлеба
Статистические методы управления качеством продукции обладают в сравнении со сплошным контролем продукции таким важным преимуществом, как возможность обнаружения отклонения от технологического процесса не тогда, когда вся партия деталей изготов ...

Эффективность природоохранных мероприятий ОАО Каравай
природоохранный загрязняющий вещество Актуальность темы исследования. Природные ресурсы и природные условия являются основой материального производства и жизнедеятельности населения. Состояние окружающей среды, качественный уровень использо ...