Статистическое изучение показателей рентабельности

Вывод.Анализ интервального ряда распределения изучаемой совокупности предприятий показывает, что распределение предприятий по прибыли от продаж не является равномерным: преобладают предприятия с прибылью от продаж от 5,1408 млн. руб. до 8,4096 млн. руб. (это 13 предприятий, доля которых составляет 43,3%); и лишь небольшое количество предприятий (по 3 в каждой группе) имеют прибыль от продаж более 11,6784 млн.руб, но менее 18,216 млн.руб., что составляет по 10% от общего числа фирм.

2. Нахождение моды и медианы полученного ряда распределения графическим методом и путем расчетов

Мода и медиана являются структурными средними величинами

, характеризующими центр распределения единиц совокупности по изучаемому признаку.

Мода Мо

для дискретного ряда - это значение признака, наиболее часто встречающееся у единиц исследуемой совокупности. В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала

(имеющего наибольшую частоту). Более точно моду можно определить графическим методом по гистограмме ряда (рис.1).

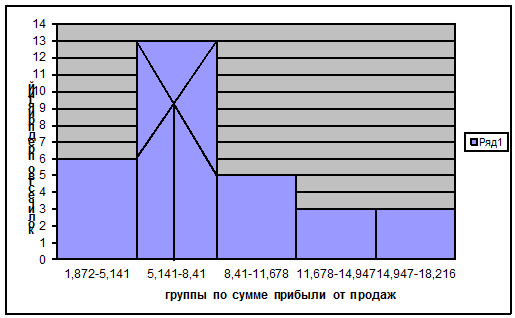
Рис. 1 Определение моды графическим методом

Конкретное значение моды для интервального ряда рассчитывается по формуле:

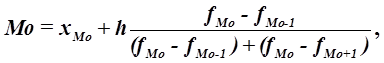
где хМo- нижняя граница модального интервала,

h

-величина модального интервала,

fMo- частота модального интервала,

fMo-1- частота интервала, предшествующего модальному,

fMo+1- частота интервала, следующего за модальным.

Согласно табл.5 модальным интервалом построенного ряда является интервал 5,1408 - 8,4096 млн. руб., так как его частота максимальна (f3 = 13):

M

0= 5,1408+3,2688*(13-6)/(13-6)+(13-5)=6,667 млн.руб.

Вывод.Для рассматриваемой совокупности предприятий наиболее распространенный размер прибыли от продаж характеризуется средней величиной 6,667 млн. руб.

Медиана Ме

- это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности. Медиану можно определить графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по накопленным частотам (табл. 5, графа 5).

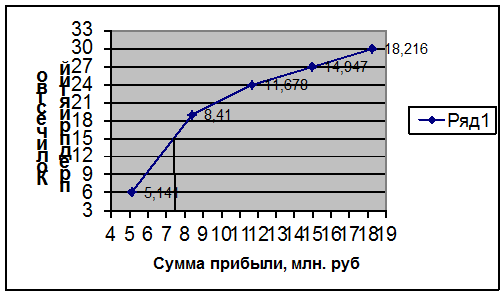
Рис. 2. Определение медианы графически методом

Конкретное значение медианы для интервального ряда рассчитывается по формуле:

,

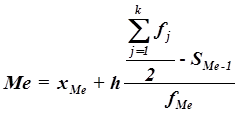где хМе

- нижняя граница медианного интервала,

h- величина медианного интервала,

- сумма всех частот,

fМе

- частота медианного интервала,

SMе-1

- кумулятивная (накопленная) частота интервала, предшествующего медианному.

Для расчета медианы необходимо, прежде всего, определить медианный интервал, для чего используются накопленные частоты (или частости) из табл. 5 (графа 5). Так как медиана делит численность ряда пополам, она будет располагаться в том интервале, где накопленная частота впервые равна

полусумме всех частот или превышает ее (т.е. все предшествующие накопленные частоты меньше этой величины). В данном примере медианным интервалом является интервал 5,1408 - 8,4096 млн. руб., так как именно в этом интервале накопленная частота Sj = 19 впервые превышает величину, равную половине численности единиц совокупности (=).

Другие материалы

Статистический анализ показателей оплаты труда на предприятии
Тема статистического анализа показателей оплаты труда является актуальной в современных условиях хозяйствования, поскольку уровень расходов на оплату труда определяет результаты производственно-хозяйственной деятельности организации. Целью д ...

Анализ производства продукции
Предприятия самостоятельно планируют свою деятельность на основе договоров, заключенных с потребителями продукции и поставщиками материально-технических ресурсов, и определяют перспективы развития исходя из спроса на производимую продукцию, раб ...