Средние величины и индексы, применение корреляционного анализа в статистике

Возможны два способа отбора: повторный - когда зафиксированная в выборке единица возвращается в генеральную совокупность, и бесповоротный отбор - когда зафиксированная единица исключается из дальнейшего просмотра и может попасть в выборку только один раз.

В задаче необходимо найти предельную ошибку. Будем использовать следующие формулы для нахождения предельной ошибки при бесповторном отборе выборки:

- для средней ;

для доли

где t - заданный коэффициент доверия;

- число единиц в выборочной совокупности;

N - число единиц в генеральной совокупности;

- дисперсия.

w - доля признака в выборочной совокупности;

- дисперсия доли признака

Предельная ошибка выборки позволяет определять предельные значения характеристик генеральной совокупности при заданной вероятности и их доверительные интервалы:

(для средней)

(для доли)

1) Расчет предельной ошибки выборки, среднего выборочного балла успеваемости.

а) Расчет среднего бала успеваемости по вузу

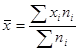=3,75

б) расчет дисперсии

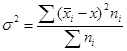= 0,79

в) расчет предельной ошибки= 2, так как вероятность = 0,954= 20+50+90+40 = 200 чел.=n*100%/5%= 4000 чел.

= 0,12

) Пределы, в которых находиться средний балл успеваемости в целом по вузу

,75-0,123,753,75+0,12

,633,753,87

) Предельная абсолютная ошибка измерения сама по себе еще не дает достаточного представления о точности проведенного эксперимента. Поэтому для оценки целесообразности и точности вычислений предельной ошибки доли студентов, которые получили неудовлетворительную или отличную оценку найдем относительную ошибку.

Относительной ошибкой называют отношение абсолютной ошибки к среднему арифметическому результату измерения. Относительную погрешность принято выражать в процентах:

Е = + (Δx/xср) 100%.

Чем меньше относительная ошибка, тем выше точность измерения.

Для студентов, получивших неудовл.:

w = 20/200=0,1 (10%)

Е = + (Δ/wср )*100%=0,04/0,1*100%=41,4%

Для студентов, получивших отлично:

w = 40/200=0,2(20%)

Е = + (Δ/wср )*100%=0,06/0,2*100%=27,6%

Величина относительной ошибки для обоих случаев (для доли студентов получивших неудовлетворительно и получивших отлично) слишком велика, поэтому производиться расчет предельной ошибки и пределов, в которых будет находиться искомое значение не целесообразно - результат будет не точный.

Задача 10

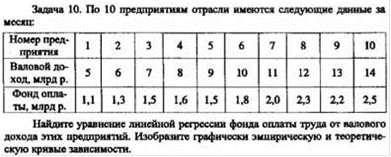
Решение.

Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями и процессами. Регрессия - это частный случай корреляции. В то время, как в корреляционном анализе оценивается сила стохастической связи, в регрессионном анализе исследуется ее форма, т.е. находится уравнение корреляционной связи (уравнение регрессии).

Другие материалы

Анализ производства продукции
Предприятия самостоятельно планируют свою деятельность на основе договоров, заключенных с потребителями продукции и поставщиками материально-технических ресурсов, и определяют перспективы развития исходя из спроса на производимую продукцию, раб ...

Статистика рынка труда, занятости и безработицы
Современный этап развития связан с новым взглядом на рабочую силу как на один из ключевых ресурсов экономики. Этот новый взгляд - свидетельство реального роста роли человеческого фактора в условиях технологического этапа НТР, когда налицо прямая ...